Speaker
Description
For unambiguous interpretation of experimental µSR data, a thorough understanding of quantum zero-point motion (ZPM) of muons in materials is essential. Namely, while ZPM of light nuclei like hydrogen and lithium is known to play a pivotal role in the structure and dynamics of many important classes of materials$^{1,2}$, quantum effects of muons in solids can be even stronger due to the lower mass of muons (~1/9 the mass of a proton) and can qualitatively change the measured µSR signal$^{3,4}$.
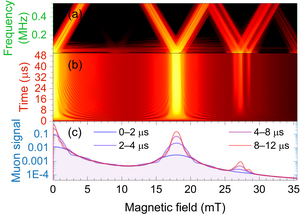
There has been much interest in using ab initio computation of muon stopping sites in materials to aid in the interpretation of µSR measurements. However, most computational techniques employed have either neglected quantum muon ZPM, or applied poorly controlled approximations to it with little clarity around the limits of their applicability. To address this, we have developed a unified description of light-particle ZPM in materials$^{4}$, clarifying the roles many-body quantum entanglement and anharmonicity play in determining the true ZPM regime. As proof of concept we applied these insights to our precision µSR quadrupolar level-crossing measurements on solid nitrogen, α–N$_2$, where they allowed us to significantly improve the accuracy of the extracted $^{14}$N nuclear quadrupolar coupling constant. This represents the first improvement in its accuracy in over 45 years, despite the ubiquity of solid nitrogen in nature, and a validation of our unified description of light-particle ZPM.
$^{1}$T. E. Markland and M. Ceriotti, Nat. Rev. Chem. 2, 0109 (2018). $^{2}$E. Snider et al., Nature 586, 373 (2020). $^{3}$S. J. Blundell, R. De Renzi, T. Lancaster and F. L. Pratt, Muon Spectroscopy: An Introduction (Oxford University Press, Oxford, 2021). $^{4}$M. Gomilšek et al., arXiv:2202.05859.